Searching for Needles in Haystacks

This is an optimization perspective to look at every single problem that we see. Inspired By professor Sicun Gao from UCSD computer science and engineering: any form of problems that we are trying to solve can be formed by an optimization scheme with a function \(f\), a domain \(X\), and a possible constraint \(C\). To name a few examples, When \(X\) is the weight space and \(f\) is just some sort of loss function, you may get any type of deep learning. When \(X\) is all possible input space and \(f\) is a function assessing badness, you have advasarial attack algorithms. If \(X\) is all possible veichle trajectories and \(f\) is a reward function, you get Reinforcement Learning or atunomous driving. If \(X\) is all posssible strings and \(f\) is the closeness metric to a prooved theorem, when having the constraint of axioms, you have mathamatical reasoning. You see, any problems can be formed as solving different instances of this problem.

\[ \begin{aligned} & \min_{x \in X} \quad F(x) \\ & \text{subject to C} \end{aligned} \]

More rigrously speaking, any act of engineering is the act of walking and searching in the infinite design space (\(\Phi(x)\), domain of things you can do, this is either deemed as action or policy parameters in RL), trying to find a good enough solution that can solve interesting problems in the problem domain (\(X\), state space) with the function metric (\(F(x)\), in metric or objective space, this is the reward model in RL or MSE objective surface in supervised learning) while caring about with the constrain (dotted line) given. You search in the parameter space that changes where you are in state space and reflecting the goodness of it in the metric space.

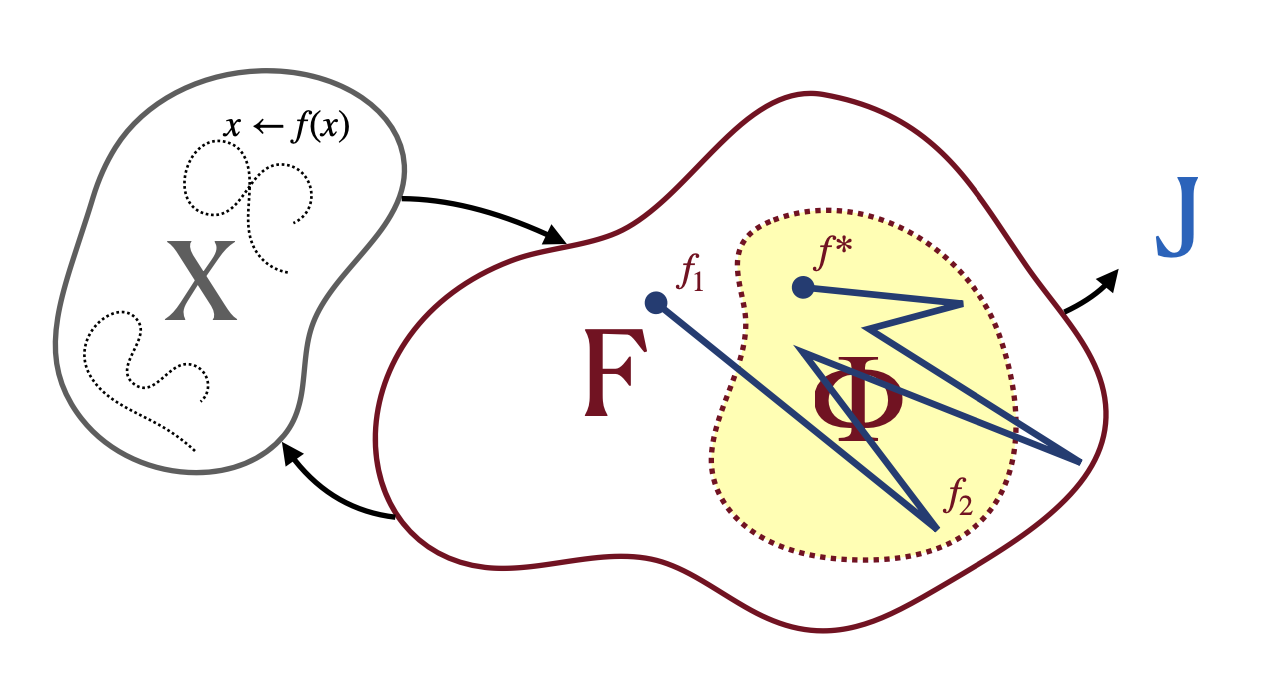
From a pessimistic perspective, these problems are NP-Hard. In the limit, they are all not solvable, we are left to face hopeless problems. But in practice, we never face the limit, with combinations of techniques, we may be able to find a good enough solution for some interesting questions. These techniques come from very different domains but some how all try to solve this same hard problem.

Some try to focus on a subset of the nice problem and intelligence stems from numerically garuantee optimality (Analytical Perspective). Some treates \(f\) itself just as a black box and doesn't care about it at all, all we need to do is randomly sample and use different techniques to ensure such sampling works. Intelligence then come from a belief that, with enough sample, we will discover some underlaying hidden struture of the environment (Statistical Perspective). And some else treats the whole problem as a puzzle to solve where logic takes us from one step to an other, if one step is wrong, we backtrack and fix. Intelligence is then logical reasoning or a tree expansion with teh constraint of logic (Combinatorics & Traditional AI Perspective)

What we so called Intelligence may just be a system happening to do the right thing for the right task. Sometimes creating something that works for an interestingly scaled level problem is the same as parsing through the fog in this vast space of interactions that give so many seemingly correct designs and finding the truth. With every try, you would explore the space a little bit more, grown the subtree a little bit deeper, and pushed more values into the table. Success never comes from one good state but rather the path you have explored and the large subtree you have built. Every single dynamic state (reference to the world and to yourself) that you have been through is not lost: The tree has been explored and nothing is lost.